15. Resonance

In the forthcoming models, the system consists of one or more CA, and it evolves as a whole. CA[600] is called stem process. It is isolated and does not interact with the environment. The stem plants other processes and controls them. They are generally short lived and called transitory processes which serve as interface between stem and the outside.

Properties of the Stem

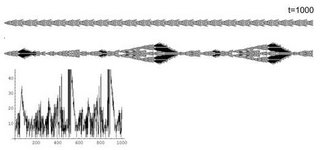
The present experiment depicts a two CA system, a stem CA[600] and a transitory process, CA[2058]. Despite its potential immortality , sooner or later it will be eliminated by the stem and replaced by a another process. The system is continually turning over. Moreover the system proceeds from solution to solution and cannot expand forever. The stem therefore curbs CA[2058]. It is controlled by the stem size. Whenever CA[2058] => k*CA[600], its boundary cells are set to zero. (k , accounts for proportionality) (v. Chapter 10 Injury)

When the stem matures it starts modulating the other CA. Following a transient they start resonating.

14. Differentiation

The following CA is controlled by rule = 2058. A zygote is planted which grows, becomes a larva and finally matures into a nectar producing adult. This evolution is called differentiation. During maturation most of the larva structure disappears and the CA is left with two cell layers which secrete nectar. Actually the mature states are one dimensional vacuoles which continually expand.

Although the zygote carries the information to produce nectar, the larva has to grow first and differentiate. If injured it may either die or never mature, as illustrated elsewhere

Actually CA[2058] is isolated and does not interact with its environment. By now you understand that in nature all creatures interact. In order rescue itself from loneliness and isolation the CA plants a new zygote. At time =25 and 12 units from its parent a zygote is planted. After a short period it interacts with its parent. Both traverse a brief transient, whereupon they jointly mature and create a solution (attractor) consisting of an invariant vacuole.

13. Memory

In its isolated state CA[600] oscillates with a period of 46. The 46 states traversed by it represent a function repertoire which may be triggered by a one bit injury (Chapter 10). The CA does not remember its past. Only the previous state is remembered, and when acted upon by rule #600 it is replaced by the present state.

The present experiment illustrates how CA-2 examines (reads) its memory and function repertoire. It plants a zygote (CA-1) and starts moving toward it (v Chapter 11). When it hits one of the CA-1 states it triggers it to perform its specific function.

The experiment was performed 46 times. At each time a CA-2 zygote was planted one time unit later than in the previous one, and the moving CA-2 hit a different CA-1 state. The image below depicts the outcome of some functions. The numbers represent CA-1 planting time. Here are the outcomes:

A. CA-1 is shifted upward to a new attractor and CA-2 dies.
B. CA-2 kills CA-1 and proceeds.
C. Both CA are annihilated and the system dies.

- CA-2 may be regarded as read/write head of the memory stored in CA-1.
- CA memory does not store data. It stores actions that are triggered by read/write head.
- Reading changes structure and with it its memory content.
- The nature of the activated function depends on the structure of the reading head.

Our organism consists of two realms: Wisdom of the Body (WOB), the site of unconscious processes, and mind. WOB stores action memories, and the conscious part of action memories is interpreted by our mind in terms of language and images.

Additional reading:
Action memory.
Orientation memory
CA memory
Ca memory
Memory of a non linear process

12. Infection

As CA move they interact and create novelty. At the beginning of each experiment two zygotes are planted. The upper matures into an isolated CA and the lower moves upward.

The numbers between them are the distances between zygotes. The numbers in front of them indicate the count which triggered the injury and movement.

I. The first encounter ended in their mutual annihilation.

II. During the second encounter, the mover triggered the upper CA to a new solution (A) which was soon replaced by the same solution of the mover (B). The CA moved at the same velocity like the triggering CA which died after triggering. This interaction might be regarded as biological collision.

III. Another biological collision. This CA cruises slower than the previous one. (v Chapter 11)

You may now explore this interaction in an applet.

11. Movement and acceleration

The 46 CA-states represent a repertoire of functions. Here we explore some which are invoked during movement. This time CA size will trigger its injury. We plant a zygote and wait until the CA matures. From then and onward, whenever the CA >=11 cells the lowest cell will be set to zero. The next CA is injured whenever its size >=13 cells, and the last, whenever its size <=19 cells.

Each injury initiates a different solution, and the CA move upward at different velocities. The smaller the CA the faster it goes. v = f[size, injury]. Suppose that the CA starts cruising at f[19,1] (1 means that only one cell was injured) . It may now accelerate its velocity by activating f[13,1], or f[11,1].

In the next image the CA started cruising upward at v=f[11,1]. At t=150 it started injuring its upper cell, leaving the lowest intact, and headed downward.

You may now examine this behavior in the following applet

10. Injury

Generally a planted zygote matures into an isolated CA. It creates its functionality by interacting with the environment. The present experiment demonstrates the reaction of the CA to injury. After the zygote has been planted the CA grows and at t = 61 it is fully mature. This state is the first in its 46 period cycle. Injury consists of setting the lowest CA bit to zero. ( additional information)The experiment was run 46 times. At each occasion a different state was injured.

1. The first CA is uninjured (isolated).
2. When the second reached state = 9 it was injured and soon died.
3. The third was injured at state = 13 whereupon it moved to a different attractor (solution).
4. Following injury at state = 17, the CA traversed a transient and then created a new solution (heart).
5. When injured at state =20 the CA entered a prolonged transient which was not followed further. Its outcome is either death or a solution.

Potential functions

The 46 states represent a repertoire of CA functions triggered by the one bit injury. Different injuries will trigger different functions. In the isolated CA the 46 states store the information on potential functions which show up when triggered by the environment.

Genotype and phenotype

All this is inherent already in the zygote, and determined by its rule = 600. You might regards the couplet {initial condition = 1, Rule =600} as the CA genotype and the various functions triggered by the environment as its phenotype. Which illustrates the relationship between genotype and phenotype in the organism. Each cell in the organism carries its genotype. Its phenotype is triggered by its immediate environment.

Additional reading on Injury and Repair

9. Movement

In order to move the CA has to change its structure, which it accomplishes by interacting with another agent. In chapter 5 the CA interacted with a barrier. Although it was displaced it soon died. In the present experiment at t = 40 the CA plants a zygote which grows until interacting with its parent. When the parent dies its progeny matures into a CA at a new location. It may then plant another zygote and its progeny moves to a different location.

From now on whenever the CA reaches t=40 (of its personal time) it plants a new zygote, and so on. Movement direction is determined by the side at which the zygote is planted.

Please note:

1. Observer time is set to zero when the experiment starts. Whenever a zygote is planted its individual time is set to zero. Every process in the system manages its own time.
More on biological time
2. The CA is symmetric and isolated. In order to act it first has to interact with another agent. Interaction creates new opportunities.
3. The isolated CA has two functions: It accumulates resources and creates progeny.
4. Displacement lasts only if the CA creates a new solution (attractor). During transient states the CA may move at great distances (Chapter 4). Its final location has to be a solution (attractor).
5. Movement proceeds from solution (attractor) to solution.

8. Observer and CA attributes

When inspecting a CA we ought to distinguish between, observer and CA attributes. In the next image a zygote was planted and the CA[600] evolves. Its history (trajectory) is outlined by the observer. It is an observer attribute. The observer plants also the zygote. The CA does not remember its history. It lives in the present (now) without any notion of the past. Nevertheless its current structure is determined by previous states, yet it does not remember them. The present state is magnified.

The next image illustrates the history of CA[600]. It is symmetric and isolated.

More information on CA[600]

7. Solution

CA histories depicted in the previous experiments are processes whose initial condition is a state containing the number 1. It is called here a zygote. You plant the zygote and the process starts evolving. Each line is a CA state at a certain moment of time. A process has three kinds of outcome:
1. Lives for ever (marked by an A in the image).
2. Dies (marked by a B in the image), or
3. Proceeds through a transient which either dies or lives for ever. (marked by a C in the image).

The study focuses on immortal processes which are called process-solutions. They are known also as attractors. We shall distinguish between regular and irregular attractors. The latter are called also strange attractors. The attractors depicted here are regular. Below is an irregular (strange) attractor.

The study explores ways which drive a process into an attractor. The experiment depicts two ways:

1. Interaction of two mortal CA ends in an immortal solution. (Second from left)
2. Interaction of a mortal and an immortal CA creates two solutions. (Last process)

Strange attractor

Click for additional information

6. Rule swapping

CA[rule] determines the transition from state to state. On the left a CA whose rule is 600. Up to time = 67 it grows whereupon it starts oscillating at a period of 46. The second CA [rule=357] lives only 88 days. The experiment explores how rule switching influences CA survival. At t=69 CA rule was switched from 357 to 600. After a transient period the CA settles at the CA[600] configuration which is called here a CA-solution.

At times t <= 69 rule swapping made the CA immortal. For t >69 rule swapping did not change the CA structure and it died at t=88.

Click for additional information

5. Interaction with a barrier

The barrier (vertical line) is made of the number 2. In the first CA history (A) the barrier was removed at day 82. The CA does not interact with it and dies on the 88^th day . Please note that the figure depicts the history of a one dimensional CA. The black line depicts the history of the barrier. At each day the barrier is placed at the same place.

In the second CA (B) the barrier was removed on day 90. The CA succeeded living somewhat longer and then died.

In the third CA (C) the barrier was removed on day 123. Initially the CA grew along the barrier, and when it was removed it regenerated and ultimately died.

During its interaction with the barrier the CA changed its structure and became a spore. This change was triggered by the barrier. Despite its new structure, the CA remembered its mature structure, which it regenerated after barrier removal.

Please note:

- The barrier represents here inert matter which is not incorporated by the CA. Nevertheless the CA uses it to remain alive and occasionally to mature and die a natural death.
- If the regenerating CA would have encountered a similar barrier, it would have continued living.
- Do you know of a modeling tool other than CA which might demonstrate a similar phenomenon?

Click here for additional experiments

4. Chaotic CA

In the following image the second CA was planted at t = 20 and distance =18. The result is an immortal chaotic CA. The graph depicts its mass accumulation (production).
Please note:
- The chaotic CA generates non chaotic and immortal progeny (attractors).
- The CA group expands indefinitely.

The next image depicts the Lorenz attractor which does not generate non-chaotic processes. You may wonder, what is the difference between this and the previous chaotic phenomenon? Currently you lack means (tools) to distinguish between them. To me, the Lorenz attractor fails to capture (portray) chaotic phenomena of nature.



Click to read more

3. Fertilization

Let’s return to the previous experiment. The planted seed is the number 1 (see chapter First Steps Oct-25). When Rule = 357 is applied to the seed it will enter its subsequent state, and so on. After some time (about 40 iterations) it will die. If you plant two seeds 22 bits apart, they will soon fuse together into one CA and become immortal and start oscillating. This simple experiment illustrates the following properties of life:

1. Fertilization
2. Emergence of a new structure.
3. Symbiosis, when the two CA fuse.
4. Their fate depends on each other.

Since if one is killed before they fuse the other will die somewhat later. Without interactiong with the other it is short lived.

Click here for the rest of this story